Abstract: The purpose of this article is to classify and compare - in essence to model - a number of different types of modelling methods employed within Operations Research and the Management Sciences (OR/MS). The classification of these methods is based on a selected number of generally recognised modelling properties. On the basis of this meta-model, requirements for the successful application of different modelling methods — for the study of given systems or objects of scientific enquiry — can be examined. The method employed for this meta-modelling task is General Morphological Analysis (GMA). The problem of a General Theory of Modelling (GTM) is also discussed.
Keywords: general theory of modelling; morphological analysis; modelling methods; OR methods
Forty years ago, as a student first of physics and then social anthropology, I would have given plenty (maybe even cut my hair) for even a simple typology of modelling methods. What a lot of time and confusion it would have saved had even a half-decent modelling typology existed. (A role model would have been McKinney's (1966) "Typology of Typologies".)
Suppose there were a GTM. What would such a theory involve? Here is my take on it, at least as concerns scientific modelling (to be sure, a qualification which is not totally clear).
By their very nature, models and modelling are subjects of study in virtually every area of science: from mathematics, physics, engineering and computer science, to psychology, sociology and the philosophy of science. I am not going to get bogged down trying to present a survey of the recent history of modelling methods. This would be a major scholarly undertaking in itself. The following are only examples from areas in which I have been involved as a modeller.
If one were to look for a GTM, one might expect to find something of the sort within the framework of Operations Research and Management Science (OR/MS) - as this field of combined research and practice has been especially interested in the issues and problems of modelling techniques for decision support. Rivett's "Principles of Model Building" (1972) is an example. Laing (1981) put forward a "Classification of Models" based on the work of Rivett, Ackoff (1979) and others, in which he categorises models along a spectrum from the purely physical to the purely mathematical. However, these and other efforts during the 1960-1980 period were directed more towards a modelling phenomenology, and Laing never claimed that he was attempting to formulate a general theory.
The development of fast, small computers, advanced graphic interfaces and new high-level programming languages created a veritable paradise for mathematical modelling. In this context, Ziegler (1984) and Ziegler et. al. (2000) offer up what they call a general theory of Modelling and Simulation (M&S - which some maliciously enjoy calling S&M). However, while this represents a huge area of study in OR/MS, it is certainly not the only area, and maybe not even the most relevant area any longer. In any event, it is interesting to note that most references to any type of general modelling theory concern "mathematical modelling and simulation". This is still the dominant feature of OR/MS and of "systems analysis" - at least in the U.S. (The fact that Horst Rittel (1972) and Russell Ackoff (1979) delivered devastating critiques of "systems analysis" and traditional "hard" OR methods for social/organisational planning problems seems to have had little impact.)
On the other side of the coin is what are called Problem Structuring Methods (PSM), developed mainly in the U.K. during the 1980's and put on the map by, among others, Jonathan Rosenhead (1989). PSM has always prescribed a wider set of modelling concepts which have been referred to (inter alia) as soft systems methodologies. (Peter Checkland's claim to this term for his particular set of techniques represents only one example.) A more general theory of conceptual modelling has also been put forward within the framework of PSM (see e.g. Kotiadis & Robinson, 2008). But, again, these do not constitute an overall framework for a GTM.
Then there is Herbert Stachowiak, and his work Allgemeine Modelltheorie (1973). Stachowiak is the German language model-guru. He presents an elaborate theory of modelling where the concept of "model" is essentially equated with the functional mapping of attributes from the so-called original (or target) onto attributes of a model. Stachowiak is clearly influenced by cybernetics and the first wave of information theory developed in the 1950's and 1960's. His approach is structural and primarily representational (although from the "non-statement view").
Unfortunately, Stachowiak's works have not been published in English. It is, of course, preposterous to demand that everything be published in English before being recognised as valuable. However, my skills in German being mediocre at best, and having only read second-hand references to Stachowiak, I am not prepared to make judgements one way or the other. If he has, in fact, formulated a viable GTM, or even put forward an important contribution to such, then his work will last and hopefully, eventually, be published in English.
There are already some indications that Stachowiak has become a source of inspiration for more contemporary theories of modelling. These have emerged since the 1990's in the areas of information science (IS), software engineering and engineering design theory. Here the intent is to go beyond mathematically based causal modelling into what has been termed multi-formalism modelling, multi-paradigm modelling and a (more or less) general theory of conceptual modelling. Examples have been put forward by e.g. Vangheluwe (2000) and Thalheim (2010).
Also, from the early 1990's come the notions of domain ontologies and domain modelling. In this context, a domain ontology is a description of the concepts and relationships that can exist for the purpose of enabling knowledge sharing and knowledge-reuse among "agents" in information systems. More specifically it represents "… the objects, concepts, and other entities that are assumed to exist in some area of interest and the relationships that hold among them" (Genesereth & Nilsson, 1987, my emphasis). The IS concept of a domain ontology was put forward in the 1980's by John McCarthy (1986) of Stanford University, and was more or less established in the early 1990's by Thomas Gruber (1995) - whose mantra has become: "an ontology is a specification of a conceptualization".
As usual, these few examples have been taken from Anglo-Saxon and European (in this case, German) research. I am sure that there have been developments towards a general modelling theory taking place elsewhere. Be that as it may, I think that I can safely state that none of the above cited sources qualifies as being called a General Theory of Modelling (GTM), at least not in the sense that I have outlined at the beginning of this paper. If this be the case, then the obvious question is: Why? With models and modelling playing such a central role in all of sci-ence, why has there not been a more concerted, "scientific" effort to develop a program for a General Theory of Modelling?
Two obvious thoughts come to mind. Firstly, maybe no GTM is even possible, due to the very nature of the concepts of a "model" and "modelling". Maybe no stable theoretical framework can be created to treat these concepts in both a (logically) consistent and (epistemologically) complete manner (analogous - and I mean only analogous - to the Gödel problem of the un-decidability of certain mathematical proofs). Although this is certainly a valid issue, I do not think that it is a practical one for what is being discussed here. We are not treating the idea of a GTM as a water-tight mathematical proof, but as a framework for a practical set of guidelines that will help us to better communicate about models and the modelling process, and by which we can carry out a critical inquiry into the requirements for valid application.
This brings us to the second possibility: that competing "schools" of basic scientific thought (e.g. the generic "realist-nominalist" dichotomy or the Naturwissenschaft-Geisteswissenschaft dichotomy) have made it difficult to agree upon a common basis for such a theory, and that those partial theories that do exist are fragmented among a number of scientific disciplines and epistemological outlooks.
In this context, one might expect that the natural sciences, and especially mathematical physics, would already have in place a domain specific GTM - this in contrast to the more "messy" Geisteswissenschaft. But this does not seem to be the case.
In 1994, Joseph Agassi presented a conference paper titled: "Why there is no theory of models" (Agassi, 1995). A student of Karl Popper, Agassi has been concerned with the history and philosophy of science and its relation to politics and ideology. In the cited paper, he is mainly concerned with the relationship between scientific models in physics and natural science, and fundamental assumptions about the natural world. But it is fully applicable to the theory of modelling in general - including models for social planning. Agassi sees our aversion to "metaphysics" as one of the main culprits:
"Metaphysics", in this context, means the epistemological-ontological assumptions that we make about the fundamental nature of the objects, relationships and processes that we are attempting to model. Agassi is saying that that our inherited aversion to dealing with this issue has led us to treat models and modelling as though these were free of such issues, naively believing that we can make the "metaphysical" issue go away if we choose not to think about it ("I feign no hypotheses").
This echoes the warning that Henri Poincaré gave us 100 years ago: The denial of ontological assumptions does not mean that we have rid ourselves of them, but that we are left with
While I certainly agree with all of this (I wrote my doctoral thesis on the subject 35 years ago), I wonder if it is the best way to approach the problem of a GTM. For, as Agassi himself has shown in much of his own writing, the history of science is the history of metaphysical politics, where it is often policy perception and ideology that define ontological assumptions, not the other way around.
This does not mean that the ontological issue should simply be dropped. However, we can make progress in the area of a GTM without first having to tackle the "metaphysical" issue for science as a whole. Instead, we can treat this problem as a methodological (and heuristic) one. Hopefully, the discussion of such methodological issues would eventually lead to a discussion about ontological assumptions, including the possibility of the expansion of present ontological categories.
Importantly, we have to look at scientific models as epistemic tools and theory generating instruments in themselves. This issue is reflected in the discussion over whether, or to what extent, models should be thought of as being primarily representational, or as being epistemic artefacts with a life of their own (see e.g. Knuuttila, 2005, 2011). There is, of course, no contradiction here; these are fully complementary roles. However, it would be a mistake to consider these as "just two different roles". The epistemic approach subsumes the representational role, as it is concerned with the epistemic means of representation - a topic that will be at the very core of any GTM.
So much by way a background. This paper does not presume to present a program for the development of a GTM. It presents only the bare-bones morphology for a class of modelling methods utilised in OR/MS. As such, it is incomplete. It is published at this time because of some uncertainty as to if, or when, a more complete morphology will be forthcoming. Also, I do not believe a single person is equipped to carry out such a study. It cries for collaboration.
Although this in itself is a very general and abstract notion of the concept of model — and is certainly not the only one that can be formulated — I feel that it suffices to illuminate the modelling principals discussed in this outline.
Note, that in earlier studies (Ritchey, 2008, 2011) I put forward a more restricted set of criteria for the notion of a (scientific) model, in which variables were required to have specified value ranges, and that the connections between variables were defined on the basis of the connections between their respective value ranges. However, this criterion has the effect of excluding a number of important descriptive modelling techniques (such as classical "influence diagrams" and analytic hierarchies) since the variables (or nodes) of these "models" can be treated as black boxes, i.e. they are not internally specified and allow for no variability. However, for the purposes of this study, this requirement is relaxed in order to explore and compare a wider variety of "modelling types". In the end, however, what is, and what is not, to be considered a scientific model is a matter of convention, as long as we make our rules clear and we apply them consistently.
On the basis of the criteria given in A and B, we abstract the following five properties:
Why have I chosen just these five properties? There are certainly other modelling properties that can be abstracted. First of all, because we have to start somewhere. But also, because these are some of the simplest operational properties that we can identify (note that P2, P3 and P4 are basic parameters in [mathematical] graph theory). A more complete morphology could certainly treat a wider range of modelling properties, including the distinctions between e.g. continuous/discrete (value ranges); deterministic/stochastic/agonistic (relationships); open/closed (modelling contexts); hierarchical/non-hierarchical (variable structure); and whether or not self-reference, whole-part interactions or so-called strong-coupling, is accounted for.
The addition of these or other properties would not necessarily increase the number of possible modelling types drastically. This is because these additional properties are not necessarily mutually orthogonal to the original five, or among themselves. They represent partially overlapping concepts. However, the need for orthogonality is not an issue here. We are examining a number of acknowledged modelling properties, and if these properties contain overlapping concepts, then this should be seen as part of the enquiry. Indeed, one of the advantages of General Morphological Analysis is that it liberates us from “enslavement to orthogonality”.
3. A morphology of modelling types
[For a detailed description of General Morphological Analysis see: http://www.swemorph.com/pdf/gma.pdf]
The five selected modelling properties make up the parameters of the morphological field in Figure 1. This field contains 64 (2 x 2 x 2 x 2 x 4) “cases” or configurations, each represented by one condition selected under each of the parameters (as in Figure 2, representing a modelling type which includes Bayesian Network models). As stated above, these properties do not necessarily represent orthogonal relationships, as some of them are partially overlapping and contain properties that are logically contradictory. A cross-consistency assessment (CCA) of these properties will allow us to identify and weed out such contradictions, thus removing from the problem space any “configurations” which contain incompatible properties.
Figure 1. Morphological field consisting of five modelling properties
Figure 2. The properties of a Bayesian Network model.
Out of necessity, I carried out this CCA solo. This is not the way it should be. Such an assessment should be done in a group setting with modelling specialists representing different competencies and traditions, and where dialogue can be established. In fact, the whole enterprise of specifying modelling properties, and “typing” the models, should be done in such a setting, in order to bring about an adequate discussion. This is basic to the morphological method.
Be this as it may, the (solo-) assessed CCA is shown in Figure 3. I chose to be extremely tolerant at this point, and only dismissed those combinations of conditions which represent blatant (logical) contradictions – i.e. “contradictions in terms” (marked by “X”). I allowed all the rest to survive – even those pairs of conditions that I couldn’t get my head around or which seemed, at least at first glance, to be “strange”. Thus we are following the anti-totalitarian principle: everything that is not expressly forbidden is allowed. It will be interesting to see if the next – Leibnizian – step is realized: “everything that is not impossible is actual”.
The deleted pairs of conditions concern the following:
Models employing mathematical functions as their connection properties must, by definition 1) have internally specified variables, 2) be quantified and 3) have (functional) direction. The 4th contradiction concerns the fact that models based on probabilistic connections are – by definition – quantified.
These four pair-wise exclusions reduce the problem space from 64 possible modelling types to 42 (a larger number of possible modelling combinations than I had originally expected). Thus, beyond these four analytical contradictions (unless I have missed something – which certainly wouldn’t surprise me), everything else is, at least, possible. One might suspect that some of these possible theoretical modelling types would be of marginal utility or just plain weird. However, as we all know, “weird” things can sometimes lead to interesting discoveries.
All of this can, and should, be questioned (for instance, the choice of the five “modelling properties” put forward here). The dream scenario would be to bring half-a-dozen (open-minded, curious) modelling specialists – all with general modelling interests but different modelling-area specialities – into a facilitated GMA workshop in order to build this “upper domain ontology” concerning modelling methods. If someone, or some organisation, is willing to sponsor/finance such an effort, I will donate my time and effort to organise and run such a workshop.
Figure 3: The Cross-Consistency Assessment of the morphological field in Figure 1.
The eight modelling methods presented (with their graphical representations) are:
Figure 4.1: A morphological model showing the properties of morphological models.
Figure 4.2: Mathematical/functional model with causal, cyclical variable relationships (as depicted in software PowerSimTM).
Figure 4.3: Bayesian network model (as depicted in software by HuginTM).
Figure 4.4:Weighted quasi-causal graph with cyclic structure (as depicted in software GammaTM.) Note: the blue connecting arrows are weighted. ).
Figure 4.5: Classical, non-quantified "influence diagram" (positive and negative influence depicted).
Figure 4.6: Non-quantified, undirected (symmetric) graph (aka "police diagram")
Figure 4.7: Probabilistic decision tree.
Figure 4.8: Un-weighted Analytic Hierarchy).
Table 1: 42 modelling types classified by way of 5 properties. Modelling types 9-42 are sorted by “type of connectivity”.
6.1 Means of representation
All models must have a means of representing the things that they are modelling – represented here by what I have called operational properties. The specification of a set of such properties is a two edged sword: On the one hand, it provides a framework for describing and classifying (i.e. “morphing”) variations in modelling types; on the other hand, it represents constraints placed on the model and the associated demands it places on the quality of the empirical information available concerning the modelling object. [Note: What modelling theory refers to as the “object”, the “original” or the “target” of the modelling process is not, of course, some “thing in itself” (the mythical ding an sich). These “objects” are themselves “models”: they are created out of our perceptions, experience and “under-standings” (i.e. hypo-theses) about the world. A model is a model of a model.]
The extent to which a specific modelling method meets the requirements for its successful application vis à vis a specific modelling object, depends on the nature of the empirical information available concerning the modelling object, and how this “matches” the properties of the modelling method. If you think that this statement is a tautological no-brainer, then there is a lot of modeling activity going on with no brains.
There are two ways to think of a “mismatch” between modelling method and modelling object.
6.2 Analysis and synthesis
Mathematician Bernhard Riemann (1826-1866) wrote his last (unfinished) work – The Mechanism of the Ear – during the spring of 1866 when he was 39 years old, and dying of tuberculosis. The unfinished manuscript was published by his friends and colleagues Ernst Weber and Gustav Fechner shortly after Riemann’s death.
The Mechanism of the Ear was written in response to the publication of Hermann Helmholtz' “On the Sensations of Tone as a Physiological Basis for the Theory of Music” (1863). Helmholtz was a leading proponent of the synthetic approach to physiology. Essentially, this approach is based upon the assumption that the study of biology can be reduced to methods based entirely upon classical (Newtonian) mechanics. On this foundation, Helmholtz developed a theory to describe the mechanism of the human ear based on careful anatomical studies and by applying the laws of acoustics as they were understood at the time. He then attempted to apply this theory to the principles of musical composition, harmony and counterpoint.
There is much in Helmholtz' study of the physiology of the ear which has been of lasting value, especially his careful anatomical investigations. However, the theory he formulated concerning the mechanism of the ear – and its premature application to the theory of musical composition – was seriously flawed.
Why, of all people, would Bernhard Riemann – the greatest mathematician of his time (some say of any time) – devote his time to the enterprise of developing an alternative theory concerning the mechanism of the ear? It concerned an issue of method. In the introduction "On the Method which is Applicable to the Study of the Physiology of the Finer Sense Organs", we see that Riemann is using this specific "case study" in order to discuss the wider applications of the analytic and the synthetic methods for scientific investigation in general. In the first 13 paragraphs of this introduction, Riemann presents an astonishing, exquisitely concise analysis of the analytic and synthetic methods. For a detailed presentation, see Ritchey (1991).
There are two ways of defining analysis and synthesis as basic scientific methods of approach: as a compositional concept and as a procedural concept. (We are not concerned here with the everyday use of the term “analysis” simply as a connotation for “investigate” or “study”.) Although the procedural concept is the more fundamental and operational, it is, unfortunately, the compositional concept that is most widely touted. As a compositional concept, analysis is defined as the procedure by which we break down an intellectual or substantial whole into parts or components. Synthesis is defined as the opposite procedure: to combine separate elements or components in order to form a coherent whole.
Careless interpretation of these definitions has sometimes led to bizarre ideas – for instance, that synthesis is "good" because it creates wholes, whereas analysis is "bad" because it reduces wholes to alienated parts. According to this view, the analytic method is regarded as belonging to reductionist tradition in science, while synthesis is seen as leading the "new way" to a holistic perspective. An example of such silliness is to be found in Russell Ackoff’s Redesigning the Future (1974):
Ackoff meant well: he was trying to get the message across that mechanistic, reductionist approaches to the study of social systems and social planning problems represent bad (social) science. However, quite aside from the fact that it is the synthetic method, not the analytic method, which is methodologically associated with a reductionist approach to scientific inquiry, such a (mis-) interpretation completely misses the point of the relationship between these two methods.
Analysis and synthesis, as scientific methods, always go hand in hand; they complement one another. Every synthesis is built upon the results of a preceding analysis, and every analysis requires a subsequent synthesis in order to verify and correct its results. In this context, to regard one method as being inherently better than the other is meaningless – tantamount to asking whether it is better to breathe in or to breathe out.
The problem with this “compositional misrepresentation” dissolves when we look at the classical, procedural notion of analysis and synthesis. Riemann clears up the compositional-procedural interplay at the beginning of his introduction (here he is referring to the “organ” as a “system” to be explained):
Riemann uses the classical, procedural definition of the concepts of analysis and synthesis, which is expressed in terms of cause and effect. We can easily see how the cause-effect relationship is translated into the compositional relationship. A system's internal processes – i.e. the interactions between its components – are regarded as the cause of what the system as a whole, or a unit, performs. What the system performs is thus the effect. From these very relationships we can immediately recognize the requirements for the application of the analytic and synthetic methods.
The synthetic approach -- i.e. to infer effects on the basis of given causes -- is therefore appro-priate when the laws and principles governing a system's internal processes are known, but when we lack a detailed picture of how the system behaves (or will behave) as a whole.
The analytical approach -- drawing conclusions about causes on the basis of effects -- is appropriate when a system's overall behavior is known, but when we do not have clear or certain knowledge about the system's internal processes or the principles governing these.
6.3 System levels
Thus this procedural definition defines two relative “system levels” (and I now take the liberty of using the term “system” as reference to a modeling “object): one from the point of view of the system’s internal components and interactions (its physiology, so to speak); and one from the point of view of its behavior as a whole, i.e. what it accomplishes, its purpose or goal (depending on what type of system we are talking about). When we have (relatively) “clear and certain knowledge” about one of these system levels there is no problem: we choose the appropriate method of attack.
However, when we work with very complex objects of enquiry (e.g. social/organizational/political systems) we often neither have a clear nor complete conception of how such a system will behave as a whole, nor fully understand all the principles and (functional) interactions at work which cause that behavior. In such cases, we must ask the important question as to which method can be regarded as more suitable as the primary method or chief point of departure. Riemann’s discussion of this issue in The Mechanism of the Ear relates importantly to how we use – and misuse – models and modelling.
We can approach this issue by considering two (ideal) reasons for building models: 1) to better understand and explain existing systems on the basis of how they work and what they do; and 2) to conceptualise and design new systems on the basis of what they should do and how best to do it. Of course, these two contrasting tasks correspond only a potiori to real-world modeling. In practice the two tasks often overlap: i.e. we attempt to understand an existing system or process in order to find ways to improve it – to re-form or re-design it. But we can use these two idealised tasks to discuss the roles of the analytic and synthetic methods in developing models.
This is easy in the case of conceptualising, designing and developing something new. When we wish to design a new system (a plant, a process, an organisation, or a policy) we seldom start out by looking at its possible components and internal interactions. We begin, instead, by asking about its purpose; its goal; what we what it to accomplish. On the basis of this, we analyse such an overreaching goal by “breaking it down” into sub-goals which we deem to be necessary requirements for fulfilling the overall goal. We then continue to break these criteria down into sub-criteria, and so forth. We stop this process when we reach the point where we are no longer defining criteria for fulfilling goal-requirements, but find ourselves starting to consider how these criteria can actually be implemented compositionally – i.e. the system’s actual physical or organisational construction. This latter question is the beginning of the synthesis phase.
What is being formulated in this process is called an analytic hierarchy, which is exactly what Thomas Saaty’s Analytical Hierarchy Process is about (AHP being one of a number of related multi-criteria decision support methods).
If the analytic approach is most appropriate as the chief point of departure for the model-ling/design of a new system, then one might imagine that the synthetic approach would best fill this role for explaining, modelling and simulating an already existing system. After all, such a system has an existing structure (composition) that one can examine in order to determine the laws of the mutual interaction of its parts, and thus to build a model that simulates its “physiology”. However, this depends entirely on the nature of the system that is the object of the modelling.
Helmholtz application of the synthetic approach – as the chief point of departure – to the study of the ear is a revealing example. Due to the limits of observation at the time, the empirical information he was able to collate did not suffice to explain some of the known psychophysical qualities of the ear (for instance the ear's enormous sensitivity and the production of overtones). He was thus led to supplement this lack of empirical (compositional) evidence by formulating a number of ad hoc hypotheses in order to complete the explanation, and thus formulate his theory (or “model”).
In his examination of Helmholtz’ method, Riemann points out that the synthetic method could very well be used successfully with the finer sense organs – as it had successfully been used with regard to the physiology of the (larger) organs of locomotion – provided that the physical characteristics of the individual parts of the sense organ could indeed be determined with requisite precision or certainty. But this was not possible at the time – and is still a great challenge today.
To make a long story short, Riemann turned Helmholtz’ study on it head: he started from a top-down analytical approach in order to “re-conceptualise” the ear on the basis of what it accomplishes. From this perspective, he could then draw certain conclusions about what a theory of the mechanism of the ear must account for, and how to test it:
He then points out that such conclusions can have universal scope, and can “give rise to advances in our knowledge of the laws of nature” -- as was the case, for example, with Euler's efforts to account for the achromatism of the eye. Here we are using the modelling process in order to tell us – or suggest – something of “added value” about the reality we are attempting to model. This is an example of the epistemic role of modelling.
[It is only very recently that the principles that Riemann was asking about have been explained, completely supporting his methodological approach. Reichenbach & Hudspeth (2010, 2011) have finally found the mechanisms at work which can explain the ear’s enormous sensitivity – the fact that is has an amplification gain of 1:4000. The authors are now in the process of “synthesising” these principles in the form of a new type of amplifier.]
6.4 Modelling self-referential systems
If the ear is difficult to model because of its microscopic-biological elusiveness, it is at least a (relatively) well-circumscribed, closed system that we can observe from the outside and which can be manipulated and tested in a (more or less) controlled manner. What about modelling social systems, which are open systems, of which we are (in many cases) a part, which cannot so easily be manipulated (in a controlled manner, that is), and which have a very special elusive quality that goes beyond any form of determined mechanism: i.e. the property of self-referential causality?
This clearly represents a case where a fundamental property of the modelling object would seem to “go beyond” the properties of any of the modelling methods presented in this study. The social/political/cognitive domain involves causative actions on society as a result of human reflexive self-reference (Bermúdez, 2000). Such “cognitive feedback” (not to be confused with how this term is sometimes used in psychology) affects interaction between macro and micro domains in the system, aka “whole-part” causality or “strong coupling”.
For modelling theory, one of the ways that this is expressed is in deliberate human actions which are motivated by the very knowledge of the model itself. Since such (meta-) actions subsume the model, the model can never predict them. Any attempt to assimilate such meta-actions or meta-actors into a new, more inclusive model will simply result in a new, more “exclusive” level of possible meta-actions. This was one of the main points brought up by Rittel (1972) concerning the failure of what he called “first generation systems analysis” as applied to social planning problems. It was (and still is) a real problem concerning stock market instability, where sophisticated models and scheming humans try to “out-meta” each other.
The only modelling method presented here which sometimes attempts to (functionally) causally model social-cognitive behaviour is System Dynamics Modelling (SDM). It is, so to speak, at the top of the food chain in our morphology. SDM was originally developed, and is applicable to, Substance Flow Analysis (SFA) and associated processes, where the parametric relationships between the components of the system are relatively well-defined and stable, and where the system is treated as closed. As a predictive model, SDM is less applicable for open-systems and where the parametric relationships between variables are not known with any precision, or where they are changing rapidly in uncertain ways. Representing causation based on human motivations is not only out of the question for SDM, but lies outside our present modelling “metaphysics”.
All of this has been thrashed about earlier, as least since Horst Rittel (1972) put forward his epistemological critique of the use of “systems analysis” for the purpose of modelling social and policy driven systems. His uncut gem of a paper – with its concept of “wicked problems” – is still one of the most enlightening discourses available. In this context, it may be that a General Theory of Modelling will more likely be driven from a policy modelling and design theoretical perspective, than from the “hard school”. In any event, it will have to be approached from “outside” our present ontological framework.
Keywords: general theory of modelling; morphological analysis; modelling methods; OR methods
1. Introduction: Why is there no General Theory of Modelling?
Why is there no general theory of modelling? By this I do not simply mean a logico-mathematical theory or a formal theory of representation. I mean an overall framework which treats of the epistemological, methodological and operational aspects of scientific modelling as a whole - from physics and biology to design theory and social planning models. No such framework seems to exist. There is no systematic (operational) classification of modelling methods; no commonly agreed upon terminology for different types of models and their properties; and no heuristic procedure or diagnostic for testing the applicability of different modelling methods for different modelling tasks. And although there are more than 100 acronyms that employ the letters GTM (including Global Traffic Manager, Gross Trading Margin and the chat marker "Giggling To Myself"), nowhere can I find GTM denoting a General Theory of Modelling.Forty years ago, as a student first of physics and then social anthropology, I would have given plenty (maybe even cut my hair) for even a simple typology of modelling methods. What a lot of time and confusion it would have saved had even a half-decent modelling typology existed. (A role model would have been McKinney's (1966) "Typology of Typologies".)
Suppose there were a GTM. What would such a theory involve? Here is my take on it, at least as concerns scientific modelling (to be sure, a qualification which is not totally clear).
- It would provide a real definition of the concept of a model, i.e. an operational definition that tells us something about how models are developed and how they operate. This, in contrast to merely nominal definitions such as "a model is an abstract representation of the thing being modelled".
- This definitional framework should be as general as possible, in order to contain the principle different types and forms of modelling methods employed in science.
- The operational definition should either include, or make it possible to abstract, a set of properties (or parameters) which indicate how models do their work, and by which different modelling methods can be classified, exemplified, compared and otherwise scrutinized.
- It would provide a framework for identifying the requirements for the successful application of different modelling methods for different modelling tasks and for different objects of scientific enquiry. It should be possible to develop a heuristic procedure - a diagnostic - to test the applicability of a given modelling method by relating the (methodological) limits of its properties to the demands of the properties of the object being modelled.
- It should give us a basis for treating models and modelling as a two-way street - a filioque, so to speak: not simply as a "means of representation", but also as epistemic tools in themselves; as instruments for hypothesis and theory generation.
- Finally, as a corollary to all of the above, it would provide a common modelling language and terminology. (Indeed, one of the most obvious indications that there is no "real" general theory of models and modelling is the simple fact that there is no generally agreed upon terminology concerning what different types of models there are, their different physiologies (so to speak) and their means of representation.)
By their very nature, models and modelling are subjects of study in virtually every area of science: from mathematics, physics, engineering and computer science, to psychology, sociology and the philosophy of science. I am not going to get bogged down trying to present a survey of the recent history of modelling methods. This would be a major scholarly undertaking in itself. The following are only examples from areas in which I have been involved as a modeller.
If one were to look for a GTM, one might expect to find something of the sort within the framework of Operations Research and Management Science (OR/MS) - as this field of combined research and practice has been especially interested in the issues and problems of modelling techniques for decision support. Rivett's "Principles of Model Building" (1972) is an example. Laing (1981) put forward a "Classification of Models" based on the work of Rivett, Ackoff (1979) and others, in which he categorises models along a spectrum from the purely physical to the purely mathematical. However, these and other efforts during the 1960-1980 period were directed more towards a modelling phenomenology, and Laing never claimed that he was attempting to formulate a general theory.
The development of fast, small computers, advanced graphic interfaces and new high-level programming languages created a veritable paradise for mathematical modelling. In this context, Ziegler (1984) and Ziegler et. al. (2000) offer up what they call a general theory of Modelling and Simulation (M&S - which some maliciously enjoy calling S&M). However, while this represents a huge area of study in OR/MS, it is certainly not the only area, and maybe not even the most relevant area any longer. In any event, it is interesting to note that most references to any type of general modelling theory concern "mathematical modelling and simulation". This is still the dominant feature of OR/MS and of "systems analysis" - at least in the U.S. (The fact that Horst Rittel (1972) and Russell Ackoff (1979) delivered devastating critiques of "systems analysis" and traditional "hard" OR methods for social/organisational planning problems seems to have had little impact.)
On the other side of the coin is what are called Problem Structuring Methods (PSM), developed mainly in the U.K. during the 1980's and put on the map by, among others, Jonathan Rosenhead (1989). PSM has always prescribed a wider set of modelling concepts which have been referred to (inter alia) as soft systems methodologies. (Peter Checkland's claim to this term for his particular set of techniques represents only one example.) A more general theory of conceptual modelling has also been put forward within the framework of PSM (see e.g. Kotiadis & Robinson, 2008). But, again, these do not constitute an overall framework for a GTM.
Then there is Herbert Stachowiak, and his work Allgemeine Modelltheorie (1973). Stachowiak is the German language model-guru. He presents an elaborate theory of modelling where the concept of "model" is essentially equated with the functional mapping of attributes from the so-called original (or target) onto attributes of a model. Stachowiak is clearly influenced by cybernetics and the first wave of information theory developed in the 1950's and 1960's. His approach is structural and primarily representational (although from the "non-statement view").
Unfortunately, Stachowiak's works have not been published in English. It is, of course, preposterous to demand that everything be published in English before being recognised as valuable. However, my skills in German being mediocre at best, and having only read second-hand references to Stachowiak, I am not prepared to make judgements one way or the other. If he has, in fact, formulated a viable GTM, or even put forward an important contribution to such, then his work will last and hopefully, eventually, be published in English.
There are already some indications that Stachowiak has become a source of inspiration for more contemporary theories of modelling. These have emerged since the 1990's in the areas of information science (IS), software engineering and engineering design theory. Here the intent is to go beyond mathematically based causal modelling into what has been termed multi-formalism modelling, multi-paradigm modelling and a (more or less) general theory of conceptual modelling. Examples have been put forward by e.g. Vangheluwe (2000) and Thalheim (2010).
Also, from the early 1990's come the notions of domain ontologies and domain modelling. In this context, a domain ontology is a description of the concepts and relationships that can exist for the purpose of enabling knowledge sharing and knowledge-reuse among "agents" in information systems. More specifically it represents "… the objects, concepts, and other entities that are assumed to exist in some area of interest and the relationships that hold among them" (Genesereth & Nilsson, 1987, my emphasis). The IS concept of a domain ontology was put forward in the 1980's by John McCarthy (1986) of Stanford University, and was more or less established in the early 1990's by Thomas Gruber (1995) - whose mantra has become: "an ontology is a specification of a conceptualization".
As usual, these few examples have been taken from Anglo-Saxon and European (in this case, German) research. I am sure that there have been developments towards a general modelling theory taking place elsewhere. Be that as it may, I think that I can safely state that none of the above cited sources qualifies as being called a General Theory of Modelling (GTM), at least not in the sense that I have outlined at the beginning of this paper. If this be the case, then the obvious question is: Why? With models and modelling playing such a central role in all of sci-ence, why has there not been a more concerted, "scientific" effort to develop a program for a General Theory of Modelling?
Two obvious thoughts come to mind. Firstly, maybe no GTM is even possible, due to the very nature of the concepts of a "model" and "modelling". Maybe no stable theoretical framework can be created to treat these concepts in both a (logically) consistent and (epistemologically) complete manner (analogous - and I mean only analogous - to the Gödel problem of the un-decidability of certain mathematical proofs). Although this is certainly a valid issue, I do not think that it is a practical one for what is being discussed here. We are not treating the idea of a GTM as a water-tight mathematical proof, but as a framework for a practical set of guidelines that will help us to better communicate about models and the modelling process, and by which we can carry out a critical inquiry into the requirements for valid application.
This brings us to the second possibility: that competing "schools" of basic scientific thought (e.g. the generic "realist-nominalist" dichotomy or the Naturwissenschaft-Geisteswissenschaft dichotomy) have made it difficult to agree upon a common basis for such a theory, and that those partial theories that do exist are fragmented among a number of scientific disciplines and epistemological outlooks.
In this context, one might expect that the natural sciences, and especially mathematical physics, would already have in place a domain specific GTM - this in contrast to the more "messy" Geisteswissenschaft. But this does not seem to be the case.
In 1994, Joseph Agassi presented a conference paper titled: "Why there is no theory of models" (Agassi, 1995). A student of Karl Popper, Agassi has been concerned with the history and philosophy of science and its relation to politics and ideology. In the cited paper, he is mainly concerned with the relationship between scientific models in physics and natural science, and fundamental assumptions about the natural world. But it is fully applicable to the theory of modelling in general - including models for social planning. Agassi sees our aversion to "metaphysics" as one of the main culprits:
| "The aversion to metaphysics led to reluctance to analyze the concept [of model - TR]. It is the concept of generalized initial conditions, which is still unclear. It cries for examination, especially in view of the dilemma of the doctrine of emergence which is now increasingly popular. First we have to give up the hostility to metaphysics and to acknowledge that at its best metaphysics is a powerful scientific heuristic and so it often acts as an ally to scientific research." (Agassi, 1995, Abstract. My emphasis). |
This echoes the warning that Henri Poincaré gave us 100 years ago: The denial of ontological assumptions does not mean that we have rid ourselves of them, but that we are left with
| "... dangerous hypotheses ... which are tacit and unconscious. Since we make them without knowing it, we are powerless to abandon them" (Poincaré, 1913). |
This does not mean that the ontological issue should simply be dropped. However, we can make progress in the area of a GTM without first having to tackle the "metaphysical" issue for science as a whole. Instead, we can treat this problem as a methodological (and heuristic) one. Hopefully, the discussion of such methodological issues would eventually lead to a discussion about ontological assumptions, including the possibility of the expansion of present ontological categories.
Importantly, we have to look at scientific models as epistemic tools and theory generating instruments in themselves. This issue is reflected in the discussion over whether, or to what extent, models should be thought of as being primarily representational, or as being epistemic artefacts with a life of their own (see e.g. Knuuttila, 2005, 2011). There is, of course, no contradiction here; these are fully complementary roles. However, it would be a mistake to consider these as "just two different roles". The epistemic approach subsumes the representational role, as it is concerned with the epistemic means of representation - a topic that will be at the very core of any GTM.
So much by way a background. This paper does not presume to present a program for the development of a GTM. It presents only the bare-bones morphology for a class of modelling methods utilised in OR/MS. As such, it is incomplete. It is published at this time because of some uncertainty as to if, or when, a more complete morphology will be forthcoming. Also, I do not believe a single person is equipped to carry out such a study. It cries for collaboration.
2. What is a scientific model?
As discussed above, the general notion of a scientific model is so broad and all-encompassing that any attempt to give it both a complete and (logically) consistent definition may be futile. For the purposes of this paper, I instead put forward what I consider to be two necessary criteria for something to be a scientific model (at least as this is usually employed in OR/MS), and then present a number of properties that emerge out of these criteria. The two criteria are:| A. | A scientific model must contain two or more mental constructs that can serve as variables i.e. dimensions which (at least potentially) can support a range of values or states (e.g. variables such as age, gender, product type, operational range). |
| B. | One must be able to establish relationships either between the variable entities as such, or between the values of the value ranges within the variables (e.g. causal, probabilistic, logical, etc.). |
Although this in itself is a very general and abstract notion of the concept of model — and is certainly not the only one that can be formulated — I feel that it suffices to illuminate the modelling principals discussed in this outline.
Note, that in earlier studies (Ritchey, 2008, 2011) I put forward a more restricted set of criteria for the notion of a (scientific) model, in which variables were required to have specified value ranges, and that the connections between variables were defined on the basis of the connections between their respective value ranges. However, this criterion has the effect of excluding a number of important descriptive modelling techniques (such as classical "influence diagrams" and analytic hierarchies) since the variables (or nodes) of these "models" can be treated as black boxes, i.e. they are not internally specified and allow for no variability. However, for the purposes of this study, this requirement is relaxed in order to explore and compare a wider variety of "modelling types". In the end, however, what is, and what is not, to be considered a scientific model is a matter of convention, as long as we make our rules clear and we apply them consistently.
On the basis of the criteria given in A and B, we abstract the following five properties:
| P1. | Specification: Are the variables of the model (1) internally specified, i.e. contain a well defined range of ordered or non-ordered values or states; or are the variables (2) unspecified and treated as black boxes? |
| P2. | Directionality: Are the connections between the variables (1) directed or (2) non-directed (symmetrical)? |
| P3. | Quantification: Are the relationships of connectivity between the variables (1) quantified or (2) non-quantified? |
| P4. | Cyclic relationships: Does the model allow for (1) cyclic connectivity (closed loops, circular feedback/recursion) between the variables, or is the model (2) acyclic? |
| P5. | Type of connectivity: What is the nature of the connective relationships between variables? Are they (1) mathematical/functional, (2) probabilistic, (3) quasi-causal (e.g. imply influence only), or (4) non-causal (e.g. logical, normative)? |
Why have I chosen just these five properties? There are certainly other modelling properties that can be abstracted. First of all, because we have to start somewhere. But also, because these are some of the simplest operational properties that we can identify (note that P2, P3 and P4 are basic parameters in [mathematical] graph theory). A more complete morphology could certainly treat a wider range of modelling properties, including the distinctions between e.g. continuous/discrete (value ranges); deterministic/stochastic/agonistic (relationships); open/closed (modelling contexts); hierarchical/non-hierarchical (variable structure); and whether or not self-reference, whole-part interactions or so-called strong-coupling, is accounted for.
The addition of these or other properties would not necessarily increase the number of possible modelling types drastically. This is because these additional properties are not necessarily mutually orthogonal to the original five, or among themselves. They represent partially overlapping concepts. However, the need for orthogonality is not an issue here. We are examining a number of acknowledged modelling properties, and if these properties contain overlapping concepts, then this should be seen as part of the enquiry. Indeed, one of the advantages of General Morphological Analysis is that it liberates us from “enslavement to orthogonality”.
3. A morphology of modelling types
[For a detailed description of General Morphological Analysis see: http://www.swemorph.com/pdf/gma.pdf]
The five selected modelling properties make up the parameters of the morphological field in Figure 1. This field contains 64 (2 x 2 x 2 x 2 x 4) “cases” or configurations, each represented by one condition selected under each of the parameters (as in Figure 2, representing a modelling type which includes Bayesian Network models). As stated above, these properties do not necessarily represent orthogonal relationships, as some of them are partially overlapping and contain properties that are logically contradictory. A cross-consistency assessment (CCA) of these properties will allow us to identify and weed out such contradictions, thus removing from the problem space any “configurations” which contain incompatible properties.
 |
 |
Out of necessity, I carried out this CCA solo. This is not the way it should be. Such an assessment should be done in a group setting with modelling specialists representing different competencies and traditions, and where dialogue can be established. In fact, the whole enterprise of specifying modelling properties, and “typing” the models, should be done in such a setting, in order to bring about an adequate discussion. This is basic to the morphological method.
Be this as it may, the (solo-) assessed CCA is shown in Figure 3. I chose to be extremely tolerant at this point, and only dismissed those combinations of conditions which represent blatant (logical) contradictions – i.e. “contradictions in terms” (marked by “X”). I allowed all the rest to survive – even those pairs of conditions that I couldn’t get my head around or which seemed, at least at first glance, to be “strange”. Thus we are following the anti-totalitarian principle: everything that is not expressly forbidden is allowed. It will be interesting to see if the next – Leibnizian – step is realized: “everything that is not impossible is actual”.
The deleted pairs of conditions concern the following:
Models employing mathematical functions as their connection properties must, by definition 1) have internally specified variables, 2) be quantified and 3) have (functional) direction. The 4th contradiction concerns the fact that models based on probabilistic connections are – by definition – quantified.
These four pair-wise exclusions reduce the problem space from 64 possible modelling types to 42 (a larger number of possible modelling combinations than I had originally expected). Thus, beyond these four analytical contradictions (unless I have missed something – which certainly wouldn’t surprise me), everything else is, at least, possible. One might suspect that some of these possible theoretical modelling types would be of marginal utility or just plain weird. However, as we all know, “weird” things can sometimes lead to interesting discoveries.
All of this can, and should, be questioned (for instance, the choice of the five “modelling properties” put forward here). The dream scenario would be to bring half-a-dozen (open-minded, curious) modelling specialists – all with general modelling interests but different modelling-area specialities – into a facilitated GMA workshop in order to build this “upper domain ontology” concerning modelling methods. If someone, or some organisation, is willing to sponsor/finance such an effort, I will donate my time and effort to organise and run such a workshop.
 |
4. Examples of modelling types
As a first test of this (meta-) model, we can plug into it a number of more or less well established or recognized modelling types. As far as I know, there is no generally agreed upon nomenclature for all of these modelling schemes. Some are clear enough – for instance Bayesian Networks – whereas others may be contested. Still others may denote rather vague categories of models such as “influence diagrams”. The names that I have chosen here are not prescriptive. If better names are available, bring them on. (One of the main purposes – and results – of morphological modelling is to develop such a common “domain terminology”.)The eight modelling methods presented (with their graphical representations) are:
- Morphological models (The meta-modelling method contains itself as a specific case.)
- System Dynamics Models
- Bayesian Network models
- Weighted influence diagram
- Un-weighted influence diagram
- Non-directed, non-quantified graph
- Probabilistic Decision Tree
- Un-weighted Analytic Hierarchy
4.1. Morphological models
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| Yes | No | No | Yes | Non-causal |
 |
4.2. System Dynamics Models
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| Yes | Yes | Yes | Yes | Math/Funct |
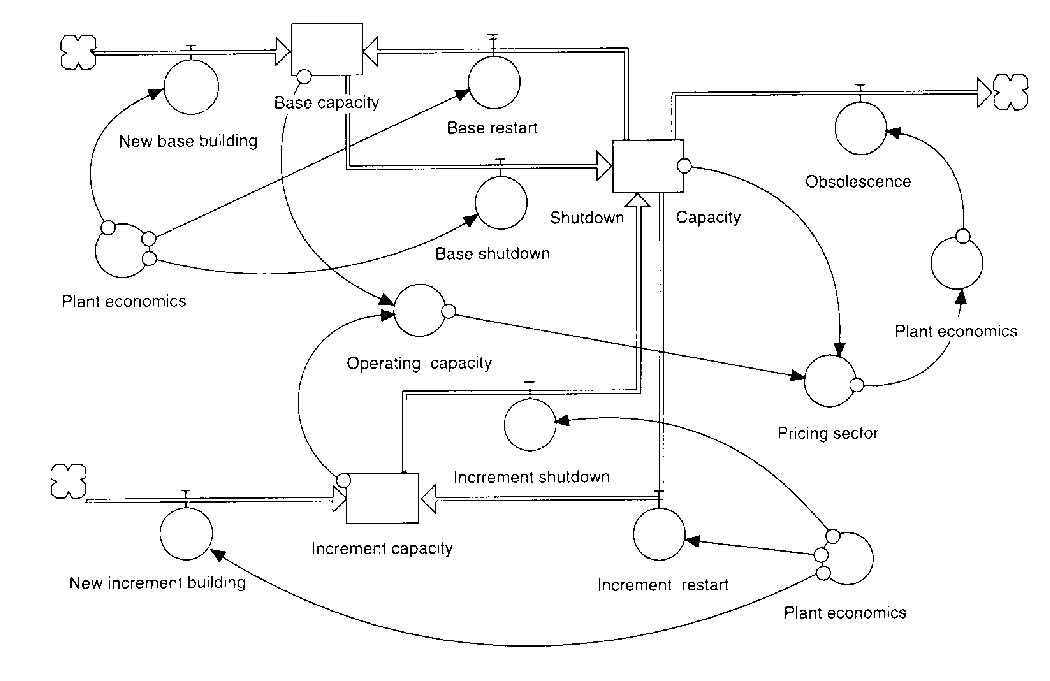 |
4.3. Bayesian Network models
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| Yes | Yes | Yes | No | Probibilistic |
 |
4.4. Weighted influence diagram (aka Vester diagram; weighted, directed graph)
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| No | Yes | Yes | Yes | Quasi-causal |
 |
4.5. Non-quantified influence diagram (Non-quantified, directed graph)
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| No | Yes | No (+/-) | Yes | Quasi-causal |
 |
4.6. Non-directed (symmetric), cyclic, non-quantified graph
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| No | No | No | Yes | Quasi-causal |
 |
4.7. Probabilistic Decision Tree
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| No | Yes | Yes | No | Probibilistic |
 |
4.8. Un-weighted Analytic Hierarchy
| Specification of values ranges |
Directional connections |
Quantification of connections |
Cyclic connections |
Type of connectivity |
| No | Yes | No | No | Non-causal |
 |
5. Table of modelling types
 |
6. Notes on the requirements for the successful application of different modelling methods
6.1 Means of representation
All models must have a means of representing the things that they are modelling – represented here by what I have called operational properties. The specification of a set of such properties is a two edged sword: On the one hand, it provides a framework for describing and classifying (i.e. “morphing”) variations in modelling types; on the other hand, it represents constraints placed on the model and the associated demands it places on the quality of the empirical information available concerning the modelling object. [Note: What modelling theory refers to as the “object”, the “original” or the “target” of the modelling process is not, of course, some “thing in itself” (the mythical ding an sich). These “objects” are themselves “models”: they are created out of our perceptions, experience and “under-standings” (i.e. hypo-theses) about the world. A model is a model of a model.]
The extent to which a specific modelling method meets the requirements for its successful application vis à vis a specific modelling object, depends on the nature of the empirical information available concerning the modelling object, and how this “matches” the properties of the modelling method. If you think that this statement is a tautological no-brainer, then there is a lot of modeling activity going on with no brains.
There are two ways to think of a “mismatch” between modelling method and modelling object.
- 1) When certain fundamental properties of the modelling object outpace (so to speak) the properties of a chosen modelling method.
- When there is evidence that there are fundamental properties that can be attributed to the modelling object that will not fit into — are not represented by — the modelling method, then any attempt to accommodate the model by ignoring these properties will result not only in short-changing the “object”: it guts its very foundation. Of course, we all know that models are “simplifications”, and represent “reality” only imperfectly. But this is not the point of contention. Contention comes into play when such a simplification discounts some basic principle governing the existence of the object. This is a fatal simplification – the point of Poincare’s argument about ontological assumptions. In this case, we need to expand the methodological domain of the modelling method to accommodate the “ontological domain” of the modelling object. The principle of “emergent qualities” (which Agassi mentioned) is a case in point.
- 2) When the properties of a chosen modelling method out-pace the quality of the information available concerning the modelling object.
- In this case, any attempted completion of this information by qualitatively “stretching” it to accommodate the model, or by imposing ad hoc teleologies, will give results that risk being completely arbitrary.
6.2 Analysis and synthesis
Mathematician Bernhard Riemann (1826-1866) wrote his last (unfinished) work – The Mechanism of the Ear – during the spring of 1866 when he was 39 years old, and dying of tuberculosis. The unfinished manuscript was published by his friends and colleagues Ernst Weber and Gustav Fechner shortly after Riemann’s death.
The Mechanism of the Ear was written in response to the publication of Hermann Helmholtz' “On the Sensations of Tone as a Physiological Basis for the Theory of Music” (1863). Helmholtz was a leading proponent of the synthetic approach to physiology. Essentially, this approach is based upon the assumption that the study of biology can be reduced to methods based entirely upon classical (Newtonian) mechanics. On this foundation, Helmholtz developed a theory to describe the mechanism of the human ear based on careful anatomical studies and by applying the laws of acoustics as they were understood at the time. He then attempted to apply this theory to the principles of musical composition, harmony and counterpoint.
There is much in Helmholtz' study of the physiology of the ear which has been of lasting value, especially his careful anatomical investigations. However, the theory he formulated concerning the mechanism of the ear – and its premature application to the theory of musical composition – was seriously flawed.
Why, of all people, would Bernhard Riemann – the greatest mathematician of his time (some say of any time) – devote his time to the enterprise of developing an alternative theory concerning the mechanism of the ear? It concerned an issue of method. In the introduction "On the Method which is Applicable to the Study of the Physiology of the Finer Sense Organs", we see that Riemann is using this specific "case study" in order to discuss the wider applications of the analytic and the synthetic methods for scientific investigation in general. In the first 13 paragraphs of this introduction, Riemann presents an astonishing, exquisitely concise analysis of the analytic and synthetic methods. For a detailed presentation, see Ritchey (1991).
There are two ways of defining analysis and synthesis as basic scientific methods of approach: as a compositional concept and as a procedural concept. (We are not concerned here with the everyday use of the term “analysis” simply as a connotation for “investigate” or “study”.) Although the procedural concept is the more fundamental and operational, it is, unfortunately, the compositional concept that is most widely touted. As a compositional concept, analysis is defined as the procedure by which we break down an intellectual or substantial whole into parts or components. Synthesis is defined as the opposite procedure: to combine separate elements or components in order to form a coherent whole.
Careless interpretation of these definitions has sometimes led to bizarre ideas – for instance, that synthesis is "good" because it creates wholes, whereas analysis is "bad" because it reduces wholes to alienated parts. According to this view, the analytic method is regarded as belonging to reductionist tradition in science, while synthesis is seen as leading the "new way" to a holistic perspective. An example of such silliness is to be found in Russell Ackoff’s Redesigning the Future (1974):
| "Machine Age thinking was analytical and based on the doctrines of reductionism and mechanism". ... Analytical thinking is a natural complement to the doctrine of reductionism. It is the mental process by which anything to be examined, hence understood, is broken down into parts." (p. 8f.) |
Analysis and synthesis, as scientific methods, always go hand in hand; they complement one another. Every synthesis is built upon the results of a preceding analysis, and every analysis requires a subsequent synthesis in order to verify and correct its results. In this context, to regard one method as being inherently better than the other is meaningless – tantamount to asking whether it is better to breathe in or to breathe out.
The problem with this “compositional misrepresentation” dissolves when we look at the classical, procedural notion of analysis and synthesis. Riemann clears up the compositional-procedural interplay at the beginning of his introduction (here he is referring to the “organ” as a “system” to be explained):
| “… there are two possible ways of gaining knowledge about the organ's [i.e. a system’s] functions. Either we can proceed from its construction, and from there seek to determine the laws of the mutual interaction of its parts as well as its response to external stimuli; or we can begin with what the organ accomplishes and then attempt to account for this. By the first route we infer effects from given causes, whereas by the second route we seek causes of given effects. Following Newton and Herbart, we can call the first route synthetic, and the second analytic. |
The synthetic approach -- i.e. to infer effects on the basis of given causes -- is therefore appro-priate when the laws and principles governing a system's internal processes are known, but when we lack a detailed picture of how the system behaves (or will behave) as a whole.
The analytical approach -- drawing conclusions about causes on the basis of effects -- is appropriate when a system's overall behavior is known, but when we do not have clear or certain knowledge about the system's internal processes or the principles governing these.
6.3 System levels
Thus this procedural definition defines two relative “system levels” (and I now take the liberty of using the term “system” as reference to a modeling “object): one from the point of view of the system’s internal components and interactions (its physiology, so to speak); and one from the point of view of its behavior as a whole, i.e. what it accomplishes, its purpose or goal (depending on what type of system we are talking about). When we have (relatively) “clear and certain knowledge” about one of these system levels there is no problem: we choose the appropriate method of attack.
However, when we work with very complex objects of enquiry (e.g. social/organizational/political systems) we often neither have a clear nor complete conception of how such a system will behave as a whole, nor fully understand all the principles and (functional) interactions at work which cause that behavior. In such cases, we must ask the important question as to which method can be regarded as more suitable as the primary method or chief point of departure. Riemann’s discussion of this issue in The Mechanism of the Ear relates importantly to how we use – and misuse – models and modelling.
We can approach this issue by considering two (ideal) reasons for building models: 1) to better understand and explain existing systems on the basis of how they work and what they do; and 2) to conceptualise and design new systems on the basis of what they should do and how best to do it. Of course, these two contrasting tasks correspond only a potiori to real-world modeling. In practice the two tasks often overlap: i.e. we attempt to understand an existing system or process in order to find ways to improve it – to re-form or re-design it. But we can use these two idealised tasks to discuss the roles of the analytic and synthetic methods in developing models.
This is easy in the case of conceptualising, designing and developing something new. When we wish to design a new system (a plant, a process, an organisation, or a policy) we seldom start out by looking at its possible components and internal interactions. We begin, instead, by asking about its purpose; its goal; what we what it to accomplish. On the basis of this, we analyse such an overreaching goal by “breaking it down” into sub-goals which we deem to be necessary requirements for fulfilling the overall goal. We then continue to break these criteria down into sub-criteria, and so forth. We stop this process when we reach the point where we are no longer defining criteria for fulfilling goal-requirements, but find ourselves starting to consider how these criteria can actually be implemented compositionally – i.e. the system’s actual physical or organisational construction. This latter question is the beginning of the synthesis phase.
What is being formulated in this process is called an analytic hierarchy, which is exactly what Thomas Saaty’s Analytical Hierarchy Process is about (AHP being one of a number of related multi-criteria decision support methods).
If the analytic approach is most appropriate as the chief point of departure for the model-ling/design of a new system, then one might imagine that the synthetic approach would best fill this role for explaining, modelling and simulating an already existing system. After all, such a system has an existing structure (composition) that one can examine in order to determine the laws of the mutual interaction of its parts, and thus to build a model that simulates its “physiology”. However, this depends entirely on the nature of the system that is the object of the modelling.
Helmholtz application of the synthetic approach – as the chief point of departure – to the study of the ear is a revealing example. Due to the limits of observation at the time, the empirical information he was able to collate did not suffice to explain some of the known psychophysical qualities of the ear (for instance the ear's enormous sensitivity and the production of overtones). He was thus led to supplement this lack of empirical (compositional) evidence by formulating a number of ad hoc hypotheses in order to complete the explanation, and thus formulate his theory (or “model”).
In his examination of Helmholtz’ method, Riemann points out that the synthetic method could very well be used successfully with the finer sense organs – as it had successfully been used with regard to the physiology of the (larger) organs of locomotion – provided that the physical characteristics of the individual parts of the sense organ could indeed be determined with requisite precision or certainty. But this was not possible at the time – and is still a great challenge today.
To make a long story short, Riemann turned Helmholtz’ study on it head: he started from a top-down analytical approach in order to “re-conceptualise” the ear on the basis of what it accomplishes. From this perspective, he could then draw certain conclusions about what a theory of the mechanism of the ear must account for, and how to test it:
| To test our explanation by reference to experience, we can in part draw upon what we have concluded about what the organ accomplishes, and in part upon what that explanation presupposes as to the physical characteristics of the organ's constituent parts. (Riemann, 1953, p. 340. My emphasis) |
[It is only very recently that the principles that Riemann was asking about have been explained, completely supporting his methodological approach. Reichenbach & Hudspeth (2010, 2011) have finally found the mechanisms at work which can explain the ear’s enormous sensitivity – the fact that is has an amplification gain of 1:4000. The authors are now in the process of “synthesising” these principles in the form of a new type of amplifier.]
6.4 Modelling self-referential systems
If the ear is difficult to model because of its microscopic-biological elusiveness, it is at least a (relatively) well-circumscribed, closed system that we can observe from the outside and which can be manipulated and tested in a (more or less) controlled manner. What about modelling social systems, which are open systems, of which we are (in many cases) a part, which cannot so easily be manipulated (in a controlled manner, that is), and which have a very special elusive quality that goes beyond any form of determined mechanism: i.e. the property of self-referential causality?
This clearly represents a case where a fundamental property of the modelling object would seem to “go beyond” the properties of any of the modelling methods presented in this study. The social/political/cognitive domain involves causative actions on society as a result of human reflexive self-reference (Bermúdez, 2000). Such “cognitive feedback” (not to be confused with how this term is sometimes used in psychology) affects interaction between macro and micro domains in the system, aka “whole-part” causality or “strong coupling”.
For modelling theory, one of the ways that this is expressed is in deliberate human actions which are motivated by the very knowledge of the model itself. Since such (meta-) actions subsume the model, the model can never predict them. Any attempt to assimilate such meta-actions or meta-actors into a new, more inclusive model will simply result in a new, more “exclusive” level of possible meta-actions. This was one of the main points brought up by Rittel (1972) concerning the failure of what he called “first generation systems analysis” as applied to social planning problems. It was (and still is) a real problem concerning stock market instability, where sophisticated models and scheming humans try to “out-meta” each other.
The only modelling method presented here which sometimes attempts to (functionally) causally model social-cognitive behaviour is System Dynamics Modelling (SDM). It is, so to speak, at the top of the food chain in our morphology. SDM was originally developed, and is applicable to, Substance Flow Analysis (SFA) and associated processes, where the parametric relationships between the components of the system are relatively well-defined and stable, and where the system is treated as closed. As a predictive model, SDM is less applicable for open-systems and where the parametric relationships between variables are not known with any precision, or where they are changing rapidly in uncertain ways. Representing causation based on human motivations is not only out of the question for SDM, but lies outside our present modelling “metaphysics”.
All of this has been thrashed about earlier, as least since Horst Rittel (1972) put forward his epistemological critique of the use of “systems analysis” for the purpose of modelling social and policy driven systems. His uncut gem of a paper – with its concept of “wicked problems” – is still one of the most enlightening discourses available. In this context, it may be that a General Theory of Modelling will more likely be driven from a policy modelling and design theoretical perspective, than from the “hard school”. In any event, it will have to be approached from “outside” our present ontological framework.
7. References and further reading
Agassi, J. (1995). "Why there is no theory of models". In William E. Herfel et al.: Theories and Models in Scientific Processes. Proceedings of AFOS '94 Workshop, August 15-26, Madralin, and IUHPS '94 Confer-ence, Warszawa, pp. 17-26.Ackoff, R. (1974) Redesigning the Future - A Systems Approach to Societal Problems. New York: Wiley.
Ackoff, R. (1979). The Future of Operational Research is Past. J. Opl. Res. Soc. Vol 30, 2, pp 93-104.
Ackoff, R & Sasieni, M. (1968). Fundamentals of Operational Research. Wiley.
Bermúdez, J. 2000. The Paradox of Self-Consciousness. MIT Press.
de Waal, A. & Ritchey, T.(2007). "Combining morphological analysis and Bayesian networks for strategic decision support." ORiON, Volume 23 (2), pp. 105-121 (2007).[Available for download at: http://www.swemorph.com/pdf/mabn.pdf. Last accesses 2012-03-09.]
Doty, D & Glick, W. (1994). Typologies as a Unique Form of Theory Building. Acad Manage Rev, 19(2).
Genesereth, M. R., & Nilsson, N. J. (1987). Logical Foundations of Artificial Intelligence. San Mateo, CA: Morgan Kaufmann Publishers.
Gruber, T. R. (1995). Toward principles for the design of ontologies used for knowledge sharing. Presented. International Journal of Human-Computer Studies, Vol. 43, Issues 4-5, pp. 907-928.
Helmholtz, H. von (1885). On the sensations of tone as a physiological basis for the theory of music. Long-mans, Green.
Kennedy, A.G. (2010). Models and Scientific Explanation. In: Philosophy of Science Assoc. 22nd Biennial Mtg., Montreal.
Knuuttila, Tarja (2005), Models as Epistemic Artefacts: Toward a Non-Representationalist Account of Scien-tific Representation.
Knuuttila, Tarja (2011), "Modeling and Representing: An Artefactual Approach", Studies in History and Phi-losophy of Science, 42:262-271.
Kotiadis, K. & Robinson, S. (2008). Conceptual Modelling: Knowledge Acquisition and Model Abstraction, Proceedings of the 2008 Winter Simulation Conference. Warwick Business School, University of Warwick
Laing, G.J. (1981). The Classification of Models. A proposal. Interndisiplinary Science Reviews, Vol. 6, No. 4, pp 355-363.
Luhmann, N. (1995). Social Systems. Stanford University Press
McCarthy, J. (1986). Circumscription-A Form Of Nonmonotonic Reasoning, Computer Science Department, Stanford University.
McKinney, John C. 1966. Constructive Typology and Social Theory. New York: Appleton-Century-Crofts.
Reichenbach. T. & Hudspeth, A. (2010). Dual contribution to amplification in the mammalian inner ear. Phys. Rev. Lett. 105, 118102.
Reichenbach. T. & Hudspeth, A. (2011). Unidirectional mechanical amplification as a design principle for an active microphone. Phys. Rev. Lett. 106, 158701.
Revitt, P. (1982). Principles of Model Building. John Wiley and Sons.
Riemann, B. (1953). Gesammelte Mathematische Werke. Dover, New York.
Riemann, B. "Mechanik des Ohres." In Riemann, B. (1953).
Ritchey, T. (1991, rev. 1996). "Analysis and Synthesis - On Scientific Method based on a Study by Bernhard Riemann". Systems Research 8(4), 21-41 (1991). [http://www.swemorph.com/pdf/anaeng-r.pdf]
Ritchey, T. (2002). "General Morphological Analysis - A general method for non-quantified modelling". Adapted from a paper presented at the 16th Euro Conference on Operational Analysis, Brussels, July 1998.[Available at: http://www.swemorph.com/pdf/gma.pdf. Last accessed 2012-03-09]
Ritchey, T. (2011). Wicked Problems/Social Messes: Decision support Modelling with Morphological Analy-sis. Springer, Berlin.
Rittel, H. (1972). "On the Planning Crisis: Systems Analysis of the 'First and Second Generations'". Bedriftsøkonomen, Nr. 8.
Rittel, H. & Webber, M. (1973). "Dilemmas in a General Theory of Planning". Policy Sciences, Vol. 4, pp 155-169. Elsevier Scientific Publishing Company, Inc: Amsterdam.
Rosenhead, J. (Ed.) (1989). Rational Analysis for a Problematic World. Wiley and Sons.
Saaty, T. (1980). The Analytic Hierarchy Process, Planning, Priority Setting, Resource Allocation. McGraw-Hill, New York.
Stachowiak, H. (1973). Allgemeine Modelltheorie, Springer Verlag, Wien.
Stachowiak, H.(1992). Modell. In Seiffert, H.; Radnitzky, G., (Eds.) (1992), Handlexikon Zur Wissenschaftstheorie, pp. 219-222. Deutscher Taschebuch Verlag GmbH & Co. KG, München.
Tarski, A. (1954). Contributions to the theory of models I, Indagationes Mathematicae 16, 572-581.
Thalheim, B. (2010). Towards a Theory of Conceptual Modelling. Journal of Universal Computer Science, vol. 16, no. 20 (2010), 3102-3137.
Vangheluwe, H. (2000). Multi-Formalism Modelling and Simulation. Proefschrift voorgedragen tot het behalen van het doctoraat in de wetenschappen. Universitiet Gent.
Zeigler, B.P. (1984) Theory of Modelling and Simulation. Robert E. Krieger, Malabar, Florida, 1984.
Ziegler B., Praehofer H. & Kim, T.G. (2000). Theory of Modelling and Simulation: Integrating Discrete Event and Continuous Complex Dynamic Systems. Academic Press, second edition, 2000.
| The Author: Dr. Tom Ritchey is a former Research Director for the Institution for Technology Foresight and Assessment at the Swedish National Defence Research Agency (FOI) in Stockholm. He is a methodologist and facilitator who works primarily with non-quantified decision support modelling -- especially with General Morphological Analysis (GMA), Bayesian Networks (BN) and Multi-Criteria Decision support. Since 1995 he has directed more than 100 projects involving computer aided MA for Swedish government agencies, national and international NGO:s and private companies. He is the founder of the Swedish Morphological Society and Director of Ritchey Consulting Inc |
This article is published by Acta Morphologica Generalis [ISSN 2001-2241] the Online Journal of the Swedish Morphological Society. It is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
