| Morphological Analysis
| Project List
| Reference List
| Download List
| Tutorial
| About Zwicky
| MA/Carma
| Glossary
| Wicked Problems
| Contact
| Credits-Links-Legal |
| Morphological Analysis
| Project List
| Reference List
| Download List
| Tutorial
| About Zwicky
| MA/Carma
| Glossary
| Wicked Problems
| Contact
| Credits-Links-Legal |
|
|
"... within the final and true world image everything is related to everything, and nothing can be discarded a priori as being unimportant." (Fritz Zwicky: Discovery, Invention, Research through the Morphological Approach, 1969.) "Morphological analysis is simply an ordered way of looking at things." (Fritz Zwicky: "Morphological Astronomy", The Observatory. Vol. 68, No. 845, Aug. 1948.)
INTRODUCTION
General Morphological Analysis (GMA) was developed by Fritz Zwicky - the Swiss astrophysicist and aerospace scientist based at the California Institute of Technology (Caltech) - as a method for structuring and investigating the total set of relationships contained in multi-dimensional, non-quantifiable, problem complexes (Zwicky 1966, 1969). Zwicky applied this method to such diverse fields as the classification of astrophysical objects, the development of jet and rocket propulsion systems, and the legal aspects of space travel and colonization. He founded the Society for Morphological Research and enthusiastically advanced the "morphological approach" for some 30 years - between the 1940's until his death in 1974 (Greenstein & Wilson, 1974). More recently, morphological analysis has been applied by a number of researchers in the USA and Europe in the field of policy analysis and futures studies (e.g. Godet, 1994; Rhyne, 1995; Coyle & McGlone, 1995; Ritchey, 1997). In 1995, advanced computer support for GMA was developed at the Swedish Defence Research Agency. This has made it possible to create interactive, non-quantified inference models, which significantly extends GMA's functionality and areas of application (see Ritchey 1998-2011). Since then, more than 100 projects have been carried out utilizing computer aided morphological analysis, for structuring complex policy and planning issues, developing scenario and strategy laboratories, and analyzing organizational and stakeholder structures. This article will begin with a discussion of some of the methodological problems confronting complex, non-quantified modeling, especially as applied to policy analysis, futures studies and technological forecasting. This is followed by a presentation of the fundamentals of the morphological approach along with an application to policy analysis. METHODOLOGICAL BACKGROUND Analyzing complex policy fields and developing futures scenarios presents us with a number of difficult methodological problems. Firstly, many, if not all of the factors involved are non-quantifiable, since they contain strong social-political dimensions and conscious self-reference among actors. This means that traditional quantitative methods, causal modeling and simulation are relatively useless. Secondly, the uncertainties inherent in such problem complexes are in principle non-reducible, and often cannot be fully described or delineated. This represents even a greater blow to the idea of causal modeling and simulation. Finally, the actual process by which conclusions are drawn in such studies is often difficult to trace - i.e. we seldom have an adequate "audit trail" describing the process of getting from initial problem formulation to specific solutions or conclusions. Without some form of traceability we have little possibility of scientific control over results, let alone reproducibility. An alternative to formal (mathematical) methods and causal modeling is a form of non-quantified modeling relying on judgemental processes and internal consistency, rather than causality. Causal modeling, when applicable, can - and should - be used as an aid to judgment. However, at a certain level of complexity (e.g. at the social, political and cognitive level), judgment must often be used -- and worked with -- more or less directly. The question is: How can judgmental processes be put on a sound methodological basis? Historically, scientific knowledge develops through cycles of analysis and synthesis: every synthesis is built upon the results of a proceeding analysis, and every analysis requires a subsequent synthesis in order to verify and correct its results (see Ritchey 1991, 2012). However, analysis and synthesis - as basic scientific methods - say nothing about a problem having to be quantifiable. Complex social-political problem fields can be analyzed into any number of non-quantified variables and ranges of conditions. Similarly, sets of non-quantified conditions can be synthesized into well-defined relationships or configurations, which represent "solution spaces". In this context, there is no fundamental difference between quantified and non-quantified modeling. GENERAL MORPHOLOGY The term morphology comes from classical Greek (morphe) and means the study of shape or form. It is concerned with the structure and arrangement of parts of an object, and how these conform (i.e. fit together) to create a whole or Gestalt. The "objects" in question can be physical (e.g. an organism or an ecology), social (e.g. an organisation or social system) or mental (e.g. linguistic forms, concepts or systems of ideas). The first to use the term morphology as an explicitly defined scientific method was J.W. von Goethe (1749-1832), especially as concerned his "comparative morphology" in botany. Today, morphology is associated with a number of scientific disciplines in which formal structure, and not primarily quantity, is a central issue. In linguistics, it is the study of word formation; in biology, it deals with the form and structure of organisms; in geology it concerns the characteristics, configuration and evolution of rocks and land forms. Fritz Zwicky proposed a generalized form of morphological research:
"Attention has been called to the fact that the term morphology has long been used in many fields of science to designate research on structural interrelations - for instance in anatomy, geology, botany and biology. ... I have proposed to generalize and systematize the concept of morphological research and include not only the study of the shapes of geometrical, geological, biological, and generally material structures, but also to study the more abstract structural interrelations among phenomena, concepts, and ideas, whatever their character might be." (Zwicky, 1966, p. 34)
Essentially, general morphological analysis is a method for identifying and investigating the total set of possible relationships or "configurations" contained in a given problem complex. In this sense, it is closely related to typology analysis, although GMA is more generalised in form and has far broader applications.
The approach begins by identifying and defining the parameters (or dimensions) of the problem complex to be investigated, and assigning each parameter a range of relevant "values" or conditions. A morphological box - also fittingly known as a "Zwicky box" - is constructed by setting the parameters against each other in an n-dimensional matrix (see Figure 1a). Each cell of the n-dimensional box contains one particular "value" or condition from each of the parameters, and thus marks out a particular state or configuration of the problem complex. For example, imagine a simple problem complex, which we define as consisting of three dimensions - let us say "colour", "texture" and "size". In order to conform to Figure 1a, let us further define the first two dimensions as consisting of 5 discrete "values" or conditions each (e.g. colour = red, green, blue, yellow, brown) and the third consisting of 3 values (size = large, medium, small) . We then have 5x5x3 (= 75) cells in the Zwicky box, each containing 3 conditions - i.e. one from each dimension (e.g. red, rough, large). The entire 3-dimensional matrix is a typological field containing all of the (formally) possible relationships involved. The typological field format utilizes the dimensions of physical space to represent its variables, as in a Cartesian coordinate system. However, the number of coordinates that can be represented in physical space ends at three. (Typologies of greater dimensions-representing hyperspaces-usually get around this problem by embedding variables within each other. However, such formats quickly become difficult to interpret, if not hopelessly unintelligible.) Employing the morphological field format (Figure 1b) liberates us from the spatial constraints of 3-dimensional space, and allows us to allocate of any number of dimensions. 
Of course, the "matrixing" of parameters, in order to uncover the multiplicity of relationships associated with a problem complex, is nothing new. The ubiquitous "four-fold table" and the study of typology construction as a classification technique attest to this fact (Bailey, 1994; Doty & Glick, 1994). However, Zwicky's highly systematic approach to multi-dimensional problem structuring turned general morphology into a discipline in itself. The method seeks both to be integrative and to explore the boundary conditions of complex problems. Used properly - and on the right types of problem complexes - the method is deceptively complex and rich.
Two simple examples of morphological analysis may suffice to illustrate the principles of the method. The first of these is an example which Zwicky himself presents in his book Discovery, Invention, Research - Through the Morphological Approach (Zwicky, 1969). As a preparatory step in the investigation of new propulsive systems, Zwicky set a list of 10 "energy forms" against itself in order to examine every possible form of energy conversion. Suppose we wanted to investigate such conversions in three steps instead of two (in this example I have shortened the list of "energy forms" to five.) Thus the matrix in Figure 2 involves 53 (=125) possible configurations. 
Figure 2: Energy Conversion Matrix (example)
For example, K->E->C can represent hydroelectric generation which is then stored in a battery. C->T->K could represent an internal combustion engine leading to energy being stored in a flywheel. E->C->T can represent a refrigerator.
Even this simple example is surprisingly complex. Zwicky examined single conversions for 10 different "energy forms" in a 2-dimensional matrix. Try it - and you will be surprised by how much you learn about energy. A second example is drawn from work that was done for the Swedish National Defence Research Agency (FOI) concerning the future of the Swedish bomb shelter program. During the Cold War period, Sweden invested large sums of money annually in the planning, building and maintenance of these shelters. With the end of the cold war, the shelter program - its form, usefulness and expense - came under greater scrutiny. This problem, which has aspects of both policy analysis and a futures study, is eminently suited for morphological analysis. The first problem was to identify and properly define the dimensions of the problem - that is to say, the relevant issues involved. These include technical, financial, political and ethical issues. One of the advantages of GMA is that there are no formal constraints to mixing and comparing such different types of issues. On the contrary, if we are really to get to the bottom of the policy problem, we must treat all relevant issues together. Secondly, for each issue (parameter), a spectrum of "values" must be defined. These values represent possible, relevant states or conditions that each parameter can assume. A segment of one of the policy spaces, which was developed for this study, is presented in Figure 3. It has been reduced from its original ten parameters to six, and is used here only for pedagogical purposes. This segment of the shelter matrix contains 2304 possible configurations, one of which is shown in the figure. (The number of possible configurations is the product of the number of conditions under each parameter: 4x4x4x3x3x4). It is fairly easy - by hand - to identify and mark out a few dozen realistic policy configurations. Examining all possible configurations, however, would take a good deal more time and effort. Furthermore, the original 10-dimensional shelter matrix contained more than 500,000 possible configurations - far too many to deal with by hand. 
Figure 3: Segment of morphological field for the Swedish bomb shelter program study, showing one of 2304 possible (formal) policy solutions.
CROSS CONSISTENCY ASSESSMENT
The next step in the analysis-synthesis process is to reduce the total set of (formally) possible configurations in the total problem space to a smaller set of internally consistent configurations representing a "solution space". This is what Zwicky called his principle of contradiction and reduction. As a procedure, I have called this the process of "cross-consistency assessment" (CCA). CCA is based upon the insight that there may be numerous pairs of conditions in the morphological field which are mutually incompatible. For instance, in the Shelter Program matrix, the condition "All (persons) take the same risk" is incompatible with that of "No geographical priority" - if it is assumed that an adversary would, indeed, make geographical priorities by concentrating on bombing larger cities or industrial centres. Similarly, the shelter philosophy of "All get same shelter quality" is not consistent with any form of geographical priority. To the extent that a particular pair of conditions is a blatant contradiction, then all those configurations containing this pair of conditions would also be internally inconsistent. To make a cross-consistency assessment, all of the parameter values (conditions) in the morphological field are compared with one another, pair-wise, in the manner of a cross-impact matrix (Figure 4, below). As each pair of conditions is examined, a judgement is made as to whether - or to what extent - the pair can coexist, i.e. represent a consistent relationship. Note that there is no reference here to causality or direction, but only to (mutual) consistency. There are three types of inconsistencies involved here: purely logical contradictions (i.e. those based on the nature of the concepts involved); empirical constraints (i.e. relationships judged be highly improbable or implausible on empirical grounds), and normative constraints (e.g. relationships ruled out on e.g. ethical or political grounds). Note, however, that it is important not to allow normative judgments to initially influence the cross-consistency assessment. For this reason, we only allow logical and empirical judgements to be made initially. Although normative judgements can, and often must, be made, they must never be confused with logical and empirical consideration. We must first discover what we judge as possible, before we make judgements about what is desirable. 
Figure 4: Cross-consistency assessment (CCA) matrix.
This technique, of using pair-wise consistency relationships between conditions to weed out internally inconsistent configurations, is made possible by a principle of dimensionally inherent in the morphological approach. While the number of configurations in a morphological field grows exponentially with each new parameter, the number of pair-wise relationships between conditions grows only as a quadratic polynomial -- or, more specifically, proportional to the triangular number series. Naturally, there are practical limits reached even with quadratic growth. The point, however, is that a morphological field involving as many as 100,000 formal configurations requires no more than a few hundred pair-wise evaluations in order to create a solution space.
The CCA reduction allows us to concentrate on a manageable number of internally consistent configurations. With dedicated software, the internally constrained morphological field becomes an inference model or virtual laboratory, where one can designate inputs, define drivers and examined resultant output configurations as elements of scenarios or specific strategies in a complex policy space. Figure 5 shows a single driver input (red) and a clustered output. In this instance, we are essentially asking the model: "Given the policy decision that every person shall have the same shelter quality, what is the option space concerning the other parameters?" Figure 6 shows a multi-driver input (red) and corresponding clustered output. 
Figure 5: Single driver configuration (Red=input; Blue=output).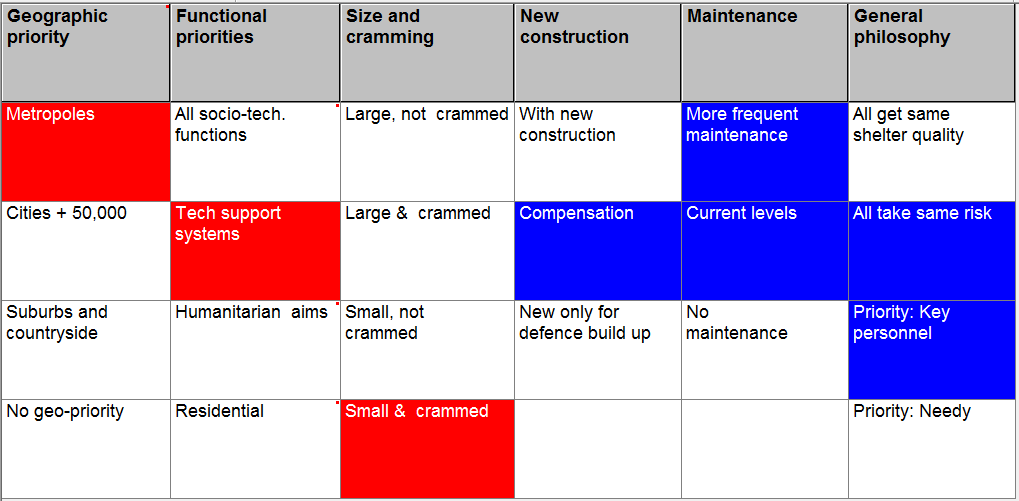 
Figure 6: Multiple driver configuration. CONCLUSIONS Morphological analysis, including the process of "cross-consistency assessment", is based on the fundamental scientific method of alternating between analysis and synthesis. For this reason, it can be trusted as a useful, non-quantified method for investigating problem complexes, which cannot be treated by formal mathematical methods, causal modeling and simulation. (For a comparison of GMA with seven other types of modeling methods employed in Operational Research and Management Science (OR/MS), see Ritchey, T. "Outline for a Morphology of Modeling Methods: Contribution to a General Theory of Modelling", Acta Morph Gen, 2012.) Zwicky called the morphological approach "totality research" which, in an "unbiased way attempts to derive all the solutions of any given problem". It may help us to discover new relationships or configurations, which may not be so evident, or which we might have overlooked by other - less systematic - methods. Importantly, it encourages the identification and investigation of boundary conditions, i.e. the limits and extremes of different contexts and factors. GMA also has definite advantages for scientific communication and - notably - for group work. As a process, the method demands that parameters, conditions and the issues underlying these be clearly defined. Poorly defined parameters become immediately (and embarrassingly) evident when they are cross-referenced and assessed for internal consistency. Such assessments simply cannot be made until the morphological field is well defined and the working group is in agreement about what these definitions mean. This is a form of garbage detection that policy analysis and futures studies certainly need more of. Finally, both the morphological field itself, and the assessments put into the cross-consistency matrix, represent a fairly clear "audit trail", which makes the judgmental processes inherent in GMA relatively traceable, and - in a certain sense - even reproducible. We have run trials in which identical morphological fields were presented to different groups for cross-consistency assessment. Comparing the results, and bringing the groups together to discuss diverging assessments, helps us to better understand the nature of the policy issues involved, and also tell us something about the effects of group composition on the assessments. The Author: Dr. Tom Ritchey is a former Research Director for the Institution for Technology Foresight and Assessment at the Swedish National Defence Research Agency (FOI) in Stockholm. He is a modelling theorist and methodologist who works primarily with non-quantified decision support modelling -- especially with General Morphological Analysis, Bayesian Networks and Multi-Criteria Decision support. Since 1995 he has directed more than 100 projects involving computer aided GMA for Swedish government agencies, national and international NGO:s and private companies. He is the founder of the Swedish Morphological Society and Director of Morphologics (formerly Ritchey Consulting). 
This article is
is licensed under a Creative Commons Attribution-NoDerivs 3.0 Unported License.
Download this article in PDF-format REFERENCES AND FURTHER READING
|
